HTW Berlin Medieninformatik

HTW Berlin
Fachbereich 4
Internationaler Bachelor Studiengang
Internationale Medieninformatik (Bachelor)
Info 2: Informatik II
Summer Term 2023

Complexity
Instead of saying

"the run time T(N) of an algorithm depending on the size of the problem N is, for all N:

T(N) = c1 · N + c2

with two constants c1 and c2"

we say:

"T(N) is of order N"

or

"T(N) is O(N)". ("Big Oh" of N)

In mathematics we say

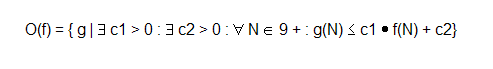
When we say that an algorithm is of order O(f), that means that it needs f units of time (in this example microseconds or millionths of a second) for computing one input, then the algorithm will need this much time for calculating N inputs:

O(f)
N

10

100

1000

10000

100000

     

O(1)

1.0 x 10 -6 s

1.0 x 10 -6 s

1.0 x 10 -6 s

1.0 x 10 -6 s

1.0 x 10 -6 s

O(log N)

1.0 x 10 -6 s

2.0 x 10 -6 s

3.0 x 10 -6 s

4.0 x 10 -6 s

5.0 x 10 -6 s

O(N)

1.0 x 10 -5 s

1.0 x 10 -4 s

1.0 x 10 -3 s

1.0 x 10 -2 s

1.0 x 10 -1 s

O(N log N)

1.0 x 10 -5 s

2.0 x 10 -4 s

3.0 x 10 -3 s

4.0 x 10 -2 s

5.0 x 10 -1 s

O(N2)

1.0 x 10 -4 s

1.0 x 10 -2 s

1.0 second

1.7 minutes

2.8 hours

O(N3)

1.0 x 10 -3 s

1.0 second

17 minutes

11.6 days

31.7 years

O(2N)

1.0 x 10 -3 s

1.0 x 10 14 century

1.0 x 10284 century

finite, but very long

finite, but very, very long

Copyright Prof. Dr. Debora Weber-Wulff
Questions or comments: <weberwu@htw-berlin.de>
Some rights reserved. CC-BY-NC-SA - Copyright and Warranty
Last change: 07.10.07 - 14:49